Něco mezi jedničkou a nulou
Mezi laickou veřejností je velmi rozšířená polopravda o fungování počítačů výhradně nad čísly 0 a 1. Ne, že by tomu tak úplně nebylo, ale platí to pouze pro tu nejnižší vrstvu. V článku přiblížím, jak fungují procesory, a popíšu práci člověka, který svým objevem tzv. fuzzy logiky navždy změnil svět.
Nejnižší vrstva
Na úrovni hardware nás bude zajímat procesor. Ten je složen z mnoha (mnoha a mnoha, klidně více než miliardy) tranzistorů, což je součástka, o které nám stačí vědět, že se vnitřně nachází v jednom ze dvou stavů. Jeden z nich označme číslem 0 a druhý číslem 1.
Co to ale znamená? Jak se dají stavy přepínat?
Pracujeme na nejnižší vrstvě, vrstvě součástek, použijeme tedy pro přepnutí napětí. Pokud do tranzistoru pustíme správnou hodnotu, která je v intervalu lišícím se pro jednotlivé procesory, dostaneme ho do stavu 1. Pokud se na vstup dostane napětí mimo vyhrazený interval, přepne se tranzistor do stavu 0.
Příklad
Řekněme, že pro stav 1 potřebujeme napětí někde mezi 1,8 V a 2,2 V. Pokud tedy přivedeme na vstup 2,1 V, přepneme tranzistor do stavu 1. Pokud přivedeme 0,1 V, přepneme ho do stavu 0.
Důvodem, proč používáme právě dva stavy, je jejich schopnost reprezentovat jakoukoliv informaci. Pomocí jedniček a nul jsem schopen zapsat číslo. A pomocí čísla napsat znak. A pomocí znaků napsat slova a věty. A pomocí těch napsat programy. Nebo články na blog.
Příklad
Třeba takové číslo 5.
zápis pomocí jedniček a nul: 101
pátý znak v abecedě: E
pátý tón ve stupnici C-dur: G
pátá barva duhy: modrá
Číslo je tedy základ. Pomocí čísel zapíšeme vše od textu, přes grafiku po zvuky.
Vidíme, že někde dole pouze nuly a jedničky jsou. Tato vrstva je ovšem tak nízko, že nás vlastně vůbec nemusí zajímat! Při používání počítače nepracujeme přímo s ní, ale právě s tím, co je nad ní. S textem, grafikou, nebo třeba zvukem.
Nuly a jedničky trochu jinak
Řekněme, že 0 bude reprezentovat logickou hodnotu false (nepravda) a 1 bude reprezentovat logickou hodnotu true (pravda). Po zavedení této konvence můžeme vyhodnocovat pravdivost výroků.
Příklad
číslo 5 je reprezentovatelné jako 101 – true; 1
po pondělku následuje úterý – true; 1
Opava je největší město České republiky – false; 0
jedna plus jedna je rovno třem – false; 0
Zatím to vypadá dobře. Máme stále jen dva stavy a teď s nimi ke všemu předtím umíme i vyjádřit, jestli něco platí nebo ne.
Ale…
Co říkáte na tohle:
- čtyřicetiletý člověk je starý,
- když je venku 18 °C je tam teplo,
- 100 Kč je hodně peněž,
- 70 km/h je vysoká rychlost.
Dá se říct, co je pravda a co ne? Obecně to nelze. Pro někoho je 18 °C ideální na kraťasy, pro někoho ne. V obytné zóně mezi paneláky a auty zaparkovanými po obou stranách silnice je 70 km/h hodně. Na dálnici při prázdné cestě je to ovšem málo. Tyto příklady se liší od těch výše. To, jestli jsou platné nebo ne, totiž ovlivňuje jejich kontext, prostředí, ve kterém o nich uvažujete. A právě tyto otázky, o kterých nelze jednoznačně rozhodnout, představovaly problém.
Fuzzy logika
Položme si otázku, jak přiblížit počítače lidskému chápání? Člověk o běžných věcech neuvažuje v ostrých mezích 0 nebo 1, pravda nebo nepravda, ano nebo ne. Máme tendence vyjadřovat se vágně, používat slůvka někde mezi jako možná nebo spíš ne.
Příklad
„Pojedeš zítra do práce autem?“ – „Nevím, asi ano.“
„Líbí se ti to tričko?“ – „Není moc pěkné.“
„Chutná ti to?“ – „Celkem ano.“
Tady nám dva stavy true a false nestačí. Chtělo by to jemnější rozdělení, které nabídne více možností k odpovědi. Co kdybychom řekli, že false bude 0, true bude 1 a možná bude 0,5? Tedy někde mezi? Toto je základní myšlenka fuzzy logiky. Zavedl ji Lotfali Askar Zadeh (Lofti A. Zadeh) roku 1973, vycházející ze své teorie fuzzy množin publikované roku 1965.

Lofti A. Zadeh
(zdroj: UC Berkeley)
Dnes je fuzzy logika použita v brzdových systémech aut, automatických regulátorech, domácích spotřebičích nebo třeba ve vyhodnocovacích systémech simulujících práci experta.
Fuzzy logika je postavena pro používání vágních pojmů. Opouštíme tedy klasickou logiku nul a jedniček (jmenuje se Booleova logika) a začínáme používat výrazy jako skoro, ne tak moc, trochu, tak trochu méně, apod. Jak už bylo řečeno výše, pro počítač musíme vymyslet způsob, jak vše převést do čísel. Přeložíme tedy výrazy na čísla v intervalu od nuly do jedné.
Příklad
„Určitě ano“ – 1
„Spíše ano“ – 0,8
„Nevím“ – 0,5
„Spíše ne“ – 0,3
„Určitě ne“ – 0
Aplikace
Často se uvádí příklad vysokého člověka.
Pro jednoduchost neuvažujme věk, původ ani konkrétní časové období.
Řekněme, že výška dospělého muže je někde mezi 50-ti centimetry a 250-ti centimetry.
O dospělém 50-ti centimetrovém člověku neřekneme „páni, ten je vysoký“, stejně jako o 250-ti centimetrovém „to je ale prcek“. Kde je ale hranice mezi velkým a malým?
Udělejme studijní odbočku do starověku. Zénon z Eleje uvedl následující problém:
Když na malou hromadu kamení přidám jeden kámen, hromada zůstane malá. Z toho vyplývá, že neexistuje velká hromada kamení.
Je to geniální myšlenka. Když si představíte velkou hromadu kamení, musíte uznat že někde na začátku, před tím než vyrostla, začínala jako malá. Začala třeba pěti kameny, na které se začaly přisypávat další.
Tedy kde je ta hranice mezi velkým a malým člověkem, mezi velkou a malou hromadou kamení?
Vraťme se k příkladu s dospělým mužem. Můžeme zůžit interval a říct, že i 150 cm měřící muž není vysoký, zatímco 190 cm měřící už ano. I 160 cm je pořád málo, zatímco někde mezi 170 cm a 180 cm začínáme pochybovat. Řekněme, že 180 cm bude zlom. Co se stane, pokud použijeme pro vyhodnocení výhradně nulu (false) a jedničku (true)?
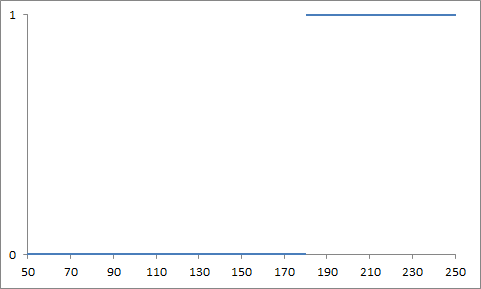
Z grafu můžeme z vodorovné osy přečíst velikost dospělého muže v centimetrech a ze svislé odpověď na otázku „je dospělý muž měřící tolik centimetrů vysoký?“.
Z grafu je vidno, že odpověď na otázku „je dospělý muž měřící 150 cm vysoký?“ je 0. Tedy false. Odpověď na jinou otázku „je dospělý muž měřící 190 cm vysoký?“ je rovna 1, tedy true. To je v pořádku.
Problém
Podle grafu a našeho zpracování pouze s použitím 0 nebo 1 je, řečeno slovně, dospělý muž
- měřící 181 cm vysoký
- měřící 179 cm malý
To je problém. Vnitřně cítíme rozdíl mezi velký a malý jako významný, ovšem v našem příkladě představuje pouhé 2 cm.
Zkusme zapojit fuzzy. Vyhraďme různě silné odpovědi a přiřaďme jim číselné hodnoty:
„Určitě ano“ – 1
„Řekl bych, že ano“ – 0,8
„Těžko říct“ – 0,5
„Řekl bych, že ne“ – 0,3
„Určitě ne“ – 0
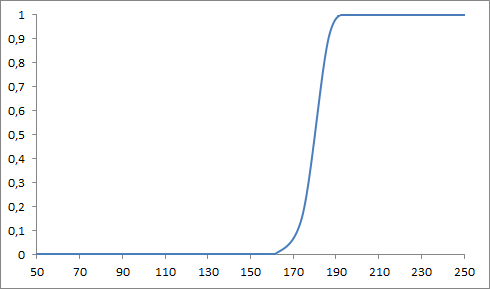
Řekněme, že u 170 cm prostě jednoznačně nevíme. Někdo by řekl vysoký, někdo ne. Přiřaďme tedy tomuto místu odpověď „Těžko říct“. Logicky pak pro hodnoty menší budou možnosti přes „Řekl bych, že ne“ po „Určite ne“. Analogicky na druhou stranu. Budeme mezi těmito stavy předpokládat hladký a postupný průběh a pro přehlednost je opět vyneseme do grafu.
Slovně ho interpretujeme tak, že výška do nějakých 160 cm určitě nedává důvod, proč nazývat dospělého muže vysokým, zatímco od cca. 190 cm o tom už není pochyb.
Výsledek
Podle druhého grafu a našeho zpracování s použitím i dalších čísel mezi 0 a 1 je, řečeno slovně, dospělý muž
- měřící 181 cm vysoký? Těžko říct.
- měřící 179 cm vysoký? Těžko říct.
To vypadá v pořádku. Vlastně jsme fuzzy přístupem smazali ostrý bod zlomu.
Čím detailněji definujeme škálu vágních pojmů, jako „spíše ne“, „víceméně ne“, „téměř ne“, „skoro určitě ne“, apod. tím přesnější dostaneme reakci.
Na naši otázku
„je dospělý muž měřící 174 cm vysoký?“
dostaneme podle výše uvedené škály od systému odpověď
„Řekl bych, že ne“
vnitrně interpretovanou jako číslo 0,19.
Závěr
Počítače umí už spousty let jednat mimo pevné hranice nuly a jedničky a rozhodovat se na základě vágních pojmů. Programy dokáží rozpoznat text psaný rukou, dokážou řídit teplotu v tavící peci, automaticky designovat součástky, dokonce i poskytnout fundovanou radu. V informatice máme celou obrovskou oblast pracující s vágností a nejistotou zvanou soft computing. Obsahuje krom fuzzy logiky obory jako neuronové sítě nebo evoluční algoritmy, které napodobují procesy fungující v přírodě.
Celá myšlenka se dá shrnout takto:
P.S. : Prof. Lofti A. Zadeh má řadu čestných doktorátů, mezi nimi i jeden z Ostravské univerzity v Ostravě.
P.P.S. : Pokud se ptáte, proč true a false nepřekládám jako pravda a lež, odpovědí je čistě formální důvod. Klidně můžete místo nepravda vidět lež.
Tags: fuzzy, informatika, Lofti A. Zadeh, matematika, soft computing



15 srpna, 2013 at 8.05
Pavle, detail ohledne tveho motivacniho prikladu formou techto tri radku:
„Pojedeš zítra do práce autem?“ – „Nevím, asi ano.“
„Líbí se ti to tričko?“ – „Není moc pěkné.“
„Chutná ti to?“ – „Celkem ano.“
Prvni radek je jina forma „uncertainty“, nicmene nejedna se o vagnost. Do te prace bud jedes autem (1) nebo nejedes (0) a nic mezitim (vynechme, ze by nekdo v pulce pichnul a dosel to pesky, na to se zjevne tazatel pokladajici otazku nepta). Dotaz nesmeruje na vagni jev, ale na ostry jev. Nicmene jev nahodny! Zde se prislusi bavit o pravdepodobnosti, zda dany jev nastane ci nikoliv.
Lepe se to vysvetluje na tahani kulicek z klobouku. Mam-li tam cervene a modre, bavim se o pravdepodobnosti, ze vytahnu cervenou (nahodny jev A) ci modrou kulicku (nahodny jev B). Vytahnu-li od slunicka vysisovanou nafialovelou kulicku, mohu zacit spekulovat, zda jsem vytahl modrou ci cervenou, tedy bavit se o stupni prislusnosti dane kulicky mezi cervene ci modre. Ale ten jev jiz nastal, ja jiz kulicku vytahnul. Neni tam zadna nahoda, nepbavim se o pravdepoodobnosti. Teorie nestoji proti sobe a v mnoha problemech se krasne doplnuji. Napriklad pokud bych mel v pytliku mnoho ruzne vysisovanych kulicek a pocital pravdepodobnost, ze vytahnu modrou, cervenou, ci prevazne modrou, alespon trochu cervenou ci jinak popsanou kulicku. Tam kombinuji jak stupne prislusnosti do danych fuzzy mnozin (cervena, prevazne modra, alespon trochu cervena apodd.) s pravdepodobnosti jejich vytazeni.
15 srpna, 2013 at 8.19
Já to záměrně popsal velmi lidově, bez nějakého nároku na matematickou preciznost. Šlo mi hlavně o pochopení myšlenky. „Pojedeš zítra autem“ uvádím jako vágní ve chvíli kdy se na to tazatel ptá. Tedy dostane odpověď „možná“ která je v dané chvíli nevyhraněná a může znamenat cokoliv. I když v konečném důsledku to bude „ano“ nebo „ne“.
Klidně můžu postavit expertní systém který položí několik otázek, jako „jste schopen řídit“, „plánujete vstanout časně“, „spěcháte do práce“, „bude venku pěkně“, apod. na které člověk nějak vágně odpoví a systém mu sdělí, že „vzhledem k předpokladům by pro vás bylo dobré jet autem“.
2 září, 2013 at 1.13
Dobrý den,
o fuzzy jsem slyšel poprvé snad před patnácti lety a rozhodně se mi ten koncept líbí. Pravdou ale je, že mi žádný takový systém nepřišel (vědomě) „do ruky“. Píšete různé příklady, že je fuzzy užito v “ brzdových systémech aut, automatických regulátorech, domácích spotřebičích nebo třeba ve vyhodnocovacích systémech simulujících práci experta“ – šel by uvést třeba odkaz na zdroj, který by ukázal, jak je skutečně fuzzy použito a proč je v daném případě lepší než klasická 0-1 logika (především ten vyhodnocovací systém simulující práci experta by mě zajímal)? A čím začít, když se chci seriózně zajímat o fuzzy?
2 září, 2013 at 11.38
Dobrý den pane Doležale,
vynasnažím se vám odpovědět co nejlépe, ovšem nezlobte se, nemůžu být ohledně některých aplikací příliš konkrétní. Nejsem si jist, kam až sahá naše NDA 🙂 Nechci též dělat reklamu konkrétním výrobkům.
Velmi známe aplikace jsou na problém obráceného kyvadla (tyčinka na natažené dlani, kterou se pohybem ruky snažíte vybalancovat) a pak orientace robota v prostoru (kdy se snaží vyhýbat překážkám). V obou těchto případech používáte vágnost pro postupné dosažení cíle.
V domácích spotřebičích je použito např. v automatických pračkách (regulace teploty a přítoku vody), nebo některých fotoaparátech (pro nastavení clony a ostření).
Obecně je fuzzy logika velmi dobře aplikována na problematiku regulátorů, kde dovoluje řídit systém „po kouskách“ a ne „po skocích“. Např. regulace teplot právě v té tavící peci.
Z více teoretického hlediska můžeme využít fuzzy např. pro práci s obrazem. Pro kompresi, detekci hran, či rekonstrukci. Ovšem to už jsou ne příliš intuitivní záležitosti.
Ohledně „systémů simulujících práci experta“. Tyto se systémy se nazývají „expertní systémy“ a pracují zhruba tak, že na začátku nějaký odborník sestaví na základě vstupních parametrů (třeba teplota) množinu pravidel, které do něj nahraje. Pravidla vypadají třeba takto „pokud je teplota nízká, pootoč koutem doprava; pokud je trochu vyšší, pootoč kohoutem trochu více doprava; …“. Poté si k němu sedne laik, a zadá „teplota je ne příliš vysoká“ načež mu systém odpoví „pootočte kohoutem trochu doprava“. Tento příklad je velmi jednoduchý, složitější (a reálné) mají mnohem více vstupů a velkou spoustu pravidel.
Jako příklad si můžete představit expertní systém, který ze vstupních parametrů týkajících se čokolád (chuť, barva, cena, vůně) odhaduje jakou má výrobek zemi původu. Tedy uživatel zadá „chuť nic moc, cena nízká, barva příliš světlá, vůně nepříjemná“ a systém odpoví „čokoláda je s vysokou pravděpodobností z Polska“ 🙂
Pro studium existuje celá škála literatury, kde však záleží na tom jestli vás láká více matematická (teoretická) stránka věci, či informatická (aplikační). Spoustu informací najdete zde:
http://irafm.osu.cz/en/c33_description/
Včetně publikací i projektů na kterých se ve fuzzy pracuje, konkrétně v IRAFM v Ostravě.
Velmi dobrou a vhodnou literaturou jsou VŠ skripta.
Např. „Expertní systémy“
http://www1.osu.cz/~klimesc/public/files/Expertni%20systemy/Expertni%20systemy_4_1.pdf
Skripta ohledně Fuzzy která jsem používal já nejsou veřejná, ale napište mi email. Poptám se autora a pokud mu to nebude vadit mohu vám je zaslat.
Jinak též existuje množství knih i v češtině, např. http://knihy.abz.cz/prodej/zaklady-fuzzy-modelovani .
19 prosince, 2014 at 23.29
Dobrý den. Mám otázku, která mi vrtá hlavou už dlouhou dobu. Počítač dokáže rozpoznat např. pravdu od nepravdy a zapsat buď číslici 0, nebo 1. Jak ale počítač pozná, že 1+1 není 3, ale 2?
28 prosince, 2014 at 11.58
Dobrý den Jarku,
odpovědí na vaši otázku jsou logické členy a dvojková soustava.
Číslo 1 je ve dvojkové soustavě 1. Máme tedy
Řekněme, že + je v tomto případě logický součet což je funkce OR. Když nahlédnete do odkazu výše uvidíte, že výsledek 1 OR 1 je 1. Řečeno slovy:
Pokud jsou oba vstupní členy rovny 1 (pravda), pak je výstup roven 1 (pravda).
Podívejte se na logický člen XOR. Uvidíte, že 1 XOR 1 je 0. Prozradím, že pro součet používáme právě XOR s přenosem jedničky do dalšího řádu. Řečeno slovy pro 1 XOR 1 s přenosem:
Pokud jsou oba vstupní členy rovny 1, pak je výstup roven 0 s přenosem 1 do dalšího řádu.
Dostáváme tedy
10 ve dvojkové soustavě je rovno 2 v soustavě desítkové. Můžete pro další příklady vyzkoušet nějakou binární kalkulačku. Případně pro detailní popis přímo nastudovat materiály k binární sčítačce.
Finta je v tom, že jsou tyto logické členy napevno zadrátované v procesoru počítače.