Tucna's blog

Rozhodl jsem se demonstrovat na příkladu z informatiky, jak probíhá výzkum a následné publikování výsledků do odborných časopisů. Zároveň tím mimoděk popíšu své téma, konkrétní studii i financování.

Téma

Budeme se zabývat částí informatiky, počítačovou grafikou. Konkrétní a už velmi úzká oblast bude rekonstrukce obrazu. Půjde nám o to, abychom z obrázku, který je poškozen, získali jiný co možná nejbližší a nejpodobnější nepoškozenému originálu. Rád uvádím pěkný příklad ze seminární práce Ing. Jiřího Zapletala.

Roku 1536 začal Michelangelo Buonarroti s malováním fresky Poslední soud, na oltářní stěnu Sixtinské kaple.

Dnes už obsahuje řadu prasklin. Co kdybychom je odstranili? S použitím počítače nemusíme fyzicky přemalovávat a riskovat tak případné (v případě informatiků až téměř jisté) znehodnocení. Označme digitálně vadná místa černou barvou.

Teď už jen provedeme kouzlo, které nahradí ony vyznačené plochy barvami.

Krom části, kdy musíme ručně vybrat poškozené oblasti, je celý průběh plně automatický. Pojďme si to kouzlo prozradit. Protože se pohybujeme v počítačové grafice, dejme důraz spíš na obrázky, než dlouhé textové, nedejbože matematické, pasáže.

Naše technika

Popíšu vše velmi lidově bez jakéhokoliv nároku na matematickou preciznost. Pokud máte náladu na hluboké studium techniky, můžete se začít do publikovaného článku uvedeného níže.

Řekněme, že malujeme obrázek použitím akvarelu. Vidíme na něm nedostatky, jako nepodařená či zcela chybějící místečka. Co kdybychom namočili prst do vody a zámazli tyto plošky barvami nanesenými kolem nich? Můžeme taky použít stejné přímo z palety a místo zamalovat. Techniku, která pracuje tímto způsobem jsme publikovali roku 2012.

Nuže, zamyslel jsem se nad otázkou:

co se stane, když vyměníme nástroj?

Co když místo prstu použijeme štětec? Nebo třeba hřebínek? Můžeme předpokládat, že zamalování dopadne pokaždé jinak. Navíc záleží i na šířce použitého nástroje. Tenký štětec obsáhne jemnější detaily, kdežto s širokým můžete pracovat rychleji. Tuto otázku máme rozpracovánu v článku z roku 2013.

Navazuje na ní další, kterou už rozeberu v tomto příspěvku.

Jak by musel vypadat nástroj, který mi dané místo opraví naprosto ideálně?

Pozadí

Je načase říct, že nástroje matematicky modelujeme tzv. bázovou funkcí. Běžně používaná je trojúhelníková. Nejde o nic zvláštního či abstraktního, je to prostě obyčejný trojúhelník.

Jeho šířka může být různá v závislosti na tom, jaký chceme dostat výstup. V této chvíli je však důležitější samotný tvar. Můžeme zvolit jiný, třeba jeden z těchto:

Oko pochází z jednoho z nejslavnějších obrázků používaných v počítačové grafice, fotky Leny Söderberg, z listopadového čísla Playboye roku 1972.

Výše položená otázka by šla přeformulovat do odbornější mluvy, jako:

existuje nějaká bazická funkce, která obecně poskytuje lepší výsledky, než běžně používaná trojúhelníková?

Narážíme na zajímavé téma. Jak poznat, co je lepší a co horší? Zkusme, pro akademické účely, sestavit speciální testovací postup. Na začátku mějme nepoškozený obrázek, třeba Lenu, který uložíme bokem. Jeho kopii nějak poškodíme a poté uvažovaným procesem automatické rekonstrukce opravíme. V této chvíli můžeme říct, že rekonstrukce dopadla úspěšně, pokud bude výstup ve shodě s nepoškozeným originálem. Tohoto stavu velmi pravděpodobně obecně nelze dosáhnout. Spokojíme se i s horším výsledkem. Otázkou je, jak míru shody změřit.

Použijeme metodu RMSE. Není nutné popisovat ji do detailu, držme se poněkud lidového přístupu. RMSE jednoduše porovnává rozdíl v barvách jednotlivých obrazových bodů (pixelů) mezi originálem a výstupem. Pokud je rozdíl nula, znamená to, že jsou stejné. Čím menší číslo, tím jsou si bližší. Celá RMSE rovna nule znamená absolutní shodu obou obrázků.

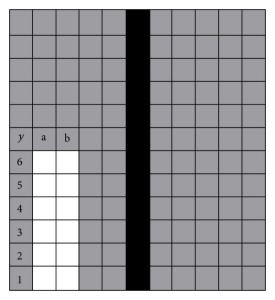
Zkusme teď uvažovat jakousi šablonu našeho nástroje, neboli bazické funkce.

Bílé pole je určeno pro vkládání bodů, kde v každém ze sloupců a a b může být právě jeden. Ostatní v šedé ploše jsou pak dopočítány automaticky tak, aby platily pro náš nástroj alespoň základní pravidla. Postupně vybereme pro oba sloupce všechny možnosti. Jeden z kroků bude, jen pro ilustraci, vypadat takto:

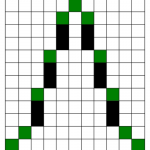
Zelené body jsou ty, co určují vlastnosti nástroje, černé slouží jen pro lepší orientaci a nemají na nic vliv.

Postupně tedy projdeme všemi možnostmi, které můžou zelené body nabývat. Každou z nich použijeme k rekonstrukci a pomocí RMSE porovnáme s nepoškozeným obrazem. Schválně si tipněte, jaký tvar u všech testovacích obrázků poskytl nejlepší výsledky.

Ještě než si předvedeme vítěze, zastavme se na chvíli nad samotnou testovací množinou. Jakkoliv je Lena používaná a vhodná, jeden obrázek by byl málo. Mohlo by se totiž stát, že zrovna u něj nástroj funguje výborně, zatímco u jiných ne. A to nechceme. Rádi bychom udělali obecnější závěr.

Zvolil jsem tyto tři:

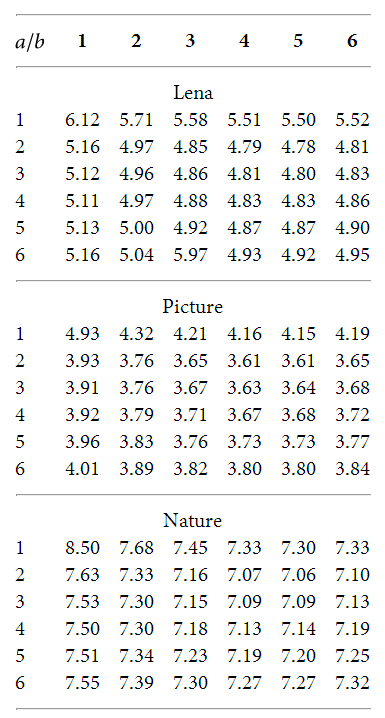
Každý je trochu jiný. Principiálně jde o sledování kvality rekonstrukce na fotce, digitální malbě a fotce se spoustou detailů. Změřil jsem tedy na těchto třech obrázcích rozdíl rekonstruovaného oproti původnímu metrikou RMSE.

Vyznat se v takové tabulce chce trochu cvičené oko. Vzpomínáte, co hodnota RMSE sleduje? Potřebujeme aby, byla co nejmenší. Podívejte se na a = 2 a b = 5. Ve všech třech obrázcích poskytuje nejlepší výstup. Vypadá následovně:

Je to, téměř přesně, lineární funkce! Ta, která se používá běžně. K čemu tedy tohle celé bylo? Nepřišli jsme na nic nového, nenašli jsme nic co by fungovalo lépe, než nástroj který se už používá.

Musíme si uvědomit, že i negativní výsledek je výsledek, a to velmi cenný! Pokud by mi někdo řekl, že používá pro rekonstrukci naší metodou klasický nástroj, ptal bych se ho „proč“? Článek je odpověď.

Věda pracuje s vyvrácením hypotéz. Řekněme, že by pro toto téma zněla

„trojúhelníková bazická funkce je perfektní pro rekonstrukci obrazu“.

Zkoušel jsem ji vyvrátit, ale bez úspěchu. Používali jsme ji v předchozích publikacích, kde se osvědčila, a ani tento test nevedl k ničemu jinému. Hypotéza tedy zatím platí.

Financování

Téma výzkumu nepovažuji za dostatečně silné pro publikování v impaktovaném časopise. Byl tedy vybrán recenzovaný Advances in Fuzzy Systems. Jak můžete vidět zde, celý proces stojí 600 $. To jsou náklady, které musím zajistit já jako autor. Můžu to zaplatit sám. Bylo by to něco jako napsat knihu, na vlastní náklady ji vydat a pak poskytovat zdarma. Zvolíme tedy jinou možnost a tu nabízejí granty.

Jako doktoranda se mě týká Studentská grantová soutěž (SGS) financovaná Ministerstvem školství, mládeže a tělovýchovy České Republiky (MŠMT). Konkrétní částky i zhodnocení jsou veřejné, můžete nahlédnout třeba na ty Ostravské univerzity v Ostravě. Já pracoval pod SGS14/PřF/2013.

Chtěl bych podotknout, že peníze, které vidíte v pravém sloupci dokumentu výše, slouží na zafinancování celého týmu, který pod grantem pracuje. Platí se z něj třeba i účasti na konferencích, v žádném případě nejde o částku jen následně přesypanou do našich kapes! Jen na okraj; u článku by mělo být vždy jasně napsáno, z jakého zdroje byl financován.

Závěr

Poznatky byly tedy sepsány a zaslány do časopisu pro podrobení recenznímu řízení. V souladu s výstupy byl upraven, doplněn a následně vydán pod názvem

Generating Suitable Basic Functions Used in Image Reconstruction by F-Transform

Můžete si ho přečíst, je k dispozici zdarma.

Článku se dá pár věcí vytknout. Prošel peer-review, přesto však může vzbuzovat pochyby.

Je RMSE opravdu vhodná metrika?

Dost zásadní otázka. Opravdu je použití prostého rozdílu (přesněji řečeno euklidovské vzdálenosti) vhodné? Jde o syrovou matematiku, mechanický proces, který bere v potaz jen samotné čísla. Existují i jiné, zmíním SSIM, který zohledňuje vnímání lidského oka. Metrika RMSE je používána a akceptována, i když se v ideálním případě doporučuje volit pro měření více technik zároveň. Pro tento článek jsem však zůstal jen u ní.

Nejsou 3 obrázky málo?

Ano, jsou. Obecně platí, že čím více, tím lépe. Recenzentům tento počet nevadil, stačí na demonstrování myšlenky, ovšem do jiného časopisu by to mohlo být málo. Jinak používáme i desítky, v jednom, na kterém právě pracujeme, necelou stovku.

Je to všechno pěkné, ale k čemu můžu rekonstrukci použít v praxi?

Možná to bude znít zvláštně, ale otázky tohoto typu se často vůbec neřeší. Je běžné, že třeba v oblasti teoretické matematiky přijde nová myšlenka, která je otestována, funguje, zatím však nikdo neví, k čemu by se mohla hodit. Je to v pořádku, nikdo nemůže vědět vše a samotná aplikace už může být dílem někoho dalšího. V našem případě použitelnost rozpracovánu máme. Konkrétně zmíněná rekonstrukce je aplikovatelná minimálně v opravě fotek; máme i další, ale prozatím se o nich nechci šířit. Nejsou ještě publikovány.

Na konec bych chtěl říct, že pokud při čtení odborného článku nemáte jasno a připadá vám, že něco není v pořádku, nebojte se kontaktovat autora. Ať už z důvodu, že potřebujete více informací, než bylo publikováno, nebo z toho, že vám předložené postupy prostě nefungují dle očekávání.

Pokud vás dané téma zajímá, nikdo vám k němu neposkytne více kvalitních informací než člověk, který stojí za výzkumem.

P.S. : Líbí se vám ten malovaný obrázek, který jsem použil jako jeden z testovacích? Tady můžete kouknout na celou galerii slečny autorky.

Tags: informatika